Hollow vesicular tissues of various sizes and shapes arise in biological organs such as ears, guts, hearts, brains and even entire organisms. Regulating their size and shape is crucial for their function. Although chemical signaling has been thought to play a role in the regulation of cellular processes that feed into larger scales, it is increasingly recognized that mechanical forces are involved in the modulation of size and shape at larger length scales. Motivated by a variety of examples of tissue cyst formation and size control that show simultaneous growth and size oscillations, we create a minimal theoretical framework for the growth and dynamics of a soft, fluid-permeable, spherical shell. We show that these shells can relieve internal pressure by bursting intermittently, shrinking and re-growing, providing a simple mechanism by which hydraulically gated oscillations can regulate size. To test our theory, we develop an in vitro experimental set-up to monitor the growth and oscillations of a hollow tissue spheroid growing freely or when confined. A simple generalization of our theory to account for irreversible deformations allows us to explain the time scales and the amplitudes of oscillations in terms of the geometry and mechanical properties of the tissue shells. Taken together, our theory and experimental observations show how soft hydraulics can regulate the size of growing tissue shells.
INTRODUCTION
Biological organs are formed via iterations and variations of just a few geometric/topological themes: folding, lumenization and segmentation. The regulation of their size and shape is crucial for normal physiological function in organisms (Conlon and Raff, 1999; Day and Lawrence, 2000; Serrano and O'Farrell, 1997). In addition to molecular and cellular chemical patterning, it is becoming increasingly clear that mechanical forces play an important role in regulating the size and shape of tissues, organs and organisms. These forces arise from differential growth or movement, confinement, and active processes such as contraction, division and apoptosis. Given the large water content in tissues, it is also likely that hydraulics plays an important role in creating and regulating size and shape at multiple levels. Indeed, at the cellular level, the role of water movements has led to a re-evaluation of cytoplasmic mechanics (Moeendarbary et al., 2013). At the organ level, we know that cysts and tubules (O'Brien et al., 2002) enclosing a central lumen are a common motif in the brain, the gut tube, the otic vesicle, kidneys, etc. (Desmond and Jacobson, 1977; Tanner et al., 1995). Fluid pressure is thought to play an important role in the early growth and shaping of vesicular structures that grow by inflation, and for an organ to become functional tissue growth and cyst growth need to be coordinated; failure to achieve this results in many diseases (Desmond and Jacobson, 1977; Navis and Bagnat, 2015; Tanner et al., 1995).
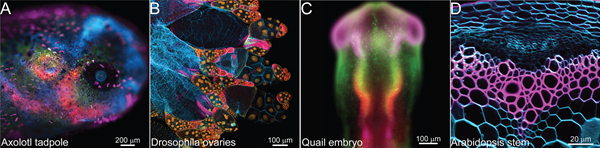
As natural occurrences of this, we note that the formation and hatching of blastocysts in amniote embryos (Biggers et al., 1988; Watson, 1992), regeneration in primitive Cnidarians such as Hydra vulgaris (Fütterer et al., 2003), and inner ear morphogenesis and stability are all dependent on tissue hydraulics (Hoijman et al., 2015). In each case, lumenization proceeds via inhomogeneous fluid pumping into an otherwise homogeneous cellular aggregate, which nucleates a cavity that then grows. In all cases, the inflated hollow cellular shell undergoes periodic oscillations in size even as it maintains an average radius stably over hours and even days (Fig. 1). For example, the blastocyst, formed after cavitation of the mammalian zygote, consists of a shell composed of two layers, the zona pellucida and the trophectoderm, that surround an internal cavity filled with fluid (Biggers et al., 1988; Watson, 1992). The blastocyst increases its total average volume via a series of slow expansions and rapid contractions during which fluid is pumped in and out (Cole, 1967; Niimura, 2003), eventually reaching a critical size before it hatches by creating a small tear in the zona pellucida that grows and allows the whole blastocyst to escape. The contractions and expansions are thought to play an active role in thinning out and softening the outer layer (Cole, 1967; Niimura, 2003). In the context of the inner ear, studies in the zebrafish suggest that hydrostatic pressure of the endolymph fluid drives early ear growth, and subsequent volume homeostasis is needed for proper function (Hoijman et al., 2015). Finally, at the level of an entire organism, young specimens of the Cnidarian H. vulgaris consist of a hollow sphere of cells that undergoes cycles of contractions and expansions driven by the hydrostatic pressure that builds up and leads to tissue bursting, causing a sudden increase of permeability (Fütterer et al., 2003; Kücken et al., 2008), followed by healing before the cycle is repeated. After several oscillations, spherical symmetry is broken causing elongation along an axis (Soriano et al., 2006). Inflation-deflation oscillations are also observed after cavitation in organoids cultured in vitro [see supplementary movies in Drost et al. (2015), Farin et al. (2016), Jaffe et al. (2008), Sato et al. (2009)], although these oscillations have not been explicitly studied in that context.
In each of these systems, which span different organs and organisms, we see that a spherical hollow tissue grows via fluid permeation and cellular division, distending until it bursts, before the cycle is repeated. This suggests that there is likely to be a common physical scenario to explain this dynamic process. Here, we provide a mathematical model that shows how hydraulically gated oscillations can provide a robust and efficient way of controlling the size of multicellular tissue cysts. To test our predictions, we introduce an in vitro experimental system for the study of oscillations in synthetic cysts and show how our general theory is consistent with our experimental observations.
RESULTS
Theory
 , so that we can approximate the opening of the hole as a sigmoid that depends on the wall stress. Then the hole has only two possible states, open and closed, and the transition between them occurs when the tension reaches the rupture tension, i.e. σ=σ2, leading to a hole of radius rb that closes when the fluid flow through the hole causes the tension to decrease to the healing tension, i.e. σ=σ1 (Fig. S3) (see supplementary information where we relax these assumptions and discuss their effects, Fig. S6). This model bears some resemblance to the one proposed for H. vulgaris regeneration (Fütterer et al., 2003; Kücken et al., 2008). However, our model accounts for tissue growth and tension-controlled rupture and healing; in the following sections, we will also introduce noise, multiple layers and different mechanical dependencies.
, so that we can approximate the opening of the hole as a sigmoid that depends on the wall stress. Then the hole has only two possible states, open and closed, and the transition between them occurs when the tension reaches the rupture tension, i.e. σ=σ2, leading to a hole of radius rb that closes when the fluid flow through the hole causes the tension to decrease to the healing tension, i.e. σ=σ1 (Fig. S3) (see supplementary information where we relax these assumptions and discuss their effects, Fig. S6). This model bears some resemblance to the one proposed for H. vulgaris regeneration (Fütterer et al., 2003; Kücken et al., 2008). However, our model accounts for tissue growth and tension-controlled rupture and healing; in the following sections, we will also introduce noise, multiple layers and different mechanical dependencies.Analysis
 ,
,  ,
,  ,
,  ,
,  . Simplifying the dimensionless system of equations, we can follow the evolution of the scaled radius, thickness and lumen pressure via the system: where
. Simplifying the dimensionless system of equations, we can follow the evolution of the scaled radius, thickness and lumen pressure via the system: where  is the dimensionless net flux,
is the dimensionless net flux,  is the dimensionless ratio between the proliferation rate and the influx rate, and
is the dimensionless ratio between the proliferation rate and the influx rate, and  is a function of the dimensionless variables that reads with e=ER0/4πηJo. We see that the dimensionless parameters that specify the dynamics are
is a function of the dimensionless variables that reads with e=ER0/4πηJo. We see that the dimensionless parameters that specify the dynamics are  (the change in volume in the spherical shell over the change relative to the internal cyst volume), ER0/ηJo (the ratio between the time scales for cyst expansion and mechanical deformation) and Δσ/E (the strain amplitude that the cyst experiences during oscillations).
(the change in volume in the spherical shell over the change relative to the internal cyst volume), ER0/ηJo (the ratio between the time scales for cyst expansion and mechanical deformation) and Δσ/E (the strain amplitude that the cyst experiences during oscillations). , neglecting for simplicity the contribution of the hydrostatic pressure to the flux, assuming it is small for soft elastic materials, i.e.
, neglecting for simplicity the contribution of the hydrostatic pressure to the flux, assuming it is small for soft elastic materials, i.e.  . For a cyst with dimensionless average radius
. For a cyst with dimensionless average radius  and amplitude of oscillations
and amplitude of oscillations  , the strain is approximately
, the strain is approximately  and: Assuming that we start with an initial cyst that is tensionless, the change in radius from the initial value R0 to the average value Ra follows: Then Eqns 10 and 11 imply that the average scaled radius and the scaled amplitude for oscillations are given by:
and: Assuming that we start with an initial cyst that is tensionless, the change in radius from the initial value R0 to the average value Ra follows: Then Eqns 10 and 11 imply that the average scaled radius and the scaled amplitude for oscillations are given by:  . Finally, the period of the oscillations, τosc, is set by the time needed to increase the cyst volume from the minimum size Rmin=Ra−ΔR/2 to the maximum size Rmax=Ra+ΔR/2: To test the validity of our simple analysis, we solve the ordinary differential equation (ODE) system Eqns 6-8 numerically for a range of parameters consistent with experiments that correspond to
. Finally, the period of the oscillations, τosc, is set by the time needed to increase the cyst volume from the minimum size Rmin=Ra−ΔR/2 to the maximum size Rmax=Ra+ΔR/2: To test the validity of our simple analysis, we solve the ordinary differential equation (ODE) system Eqns 6-8 numerically for a range of parameters consistent with experiments that correspond to  , e=9.28 · 1012,
, e=9.28 · 1012,  ,
,  ,
,  ,
,  . In Fig. 2B, we show a set of trajectories for the variations of R, h, σ and P; as expected, the cyst grows from an initial state and then starts to oscillate asymmetrically because the time scale for rupture is much faster than that of growth. Consistent with our scaling predictions (Fig. S4), we see that both the radius and the tension oscillate with period τosc around a constant value after an initial increase. We also see that the cyst thickness and pressure can increase or decrease during the first stage before oscillations appear, depending on the ratio
. In Fig. 2B, we show a set of trajectories for the variations of R, h, σ and P; as expected, the cyst grows from an initial state and then starts to oscillate asymmetrically because the time scale for rupture is much faster than that of growth. Consistent with our scaling predictions (Fig. S4), we see that both the radius and the tension oscillate with period τosc around a constant value after an initial increase. We also see that the cyst thickness and pressure can increase or decrease during the first stage before oscillations appear, depending on the ratio  and the initial values h0, R0 and P0 (see Eqn 7). If the initial tension and pressure are different from zero, this will affect the initial growth phase, and yield a different value for the maximum size, but all our qualitative results will remain similar. When the cells in the shell proliferate Jc≠0; the average values of the pressure and thickness, as well as the amplitude of their oscillations increase linearly, consistent with our analytical estimates (Eqns 14, 15).
and the initial values h0, R0 and P0 (see Eqn 7). If the initial tension and pressure are different from zero, this will affect the initial growth phase, and yield a different value for the maximum size, but all our qualitative results will remain similar. When the cells in the shell proliferate Jc≠0; the average values of the pressure and thickness, as well as the amplitude of their oscillations increase linearly, consistent with our analytical estimates (Eqns 14, 15).Experiments
To test these theoretical ideas in an experimental setting, we developed an artificial set-up using multicellular cysts for which oscillations and growth can be easily monitored. Cysts were prepared from MCF10-DCIS.com cells using the Cellular Capsules Technology as described by Alessandri et al. (2013) for multicellular spheroids (see schematics in Fig. 3A). Briefly, a composite fluid jet is generated using a co-extrusion method with cells in suspension in the core flow and a polysaccharide (alginate) that undergoes gelation in contact with divalent ions in the sheath flow. Following encapsulation, we observe that cells which are confined in the aqueous core of the hollow permeable capsule divide and occupy an increasing volume of the capsule. Confocal micrographs of the equatorial plane of the encapsulated multicellular aggregates show that the spheroids are hollow (Fig. S1). Confocal live imaging of the cyst surface also reveals a honeycomb-like structure, which is typical of epithelia (Movie 1).
We further monitored the growth dynamics of individual cysts by phase contrast microscopy by acquiring time-lapse sequences over extended periods of times (∼15 days). Fig. 1C and Movies 2-4 show typical sequences of cyst oscillations. We immediately remark that cyst average radii increase in time from one cycle to another with several different scenarios seen: (1) when Rcyst<Rcapsule, the cyst expands and shrinks freely (Movie 2); (2) when Rcyst>Rcapsule, the cyst expands against an elastic micro-compartment (Movie 3); (3) for large deformations of the capsules, the capsule occasionally bursts out and the cyst may escape (a phenomenon that is strongly reminiscent of blastocyst hatching in embryos), before resuming free oscillations (Movie 4). We also observe that the oscillation amplitude and period are altered once the cyst reaches the wall of the capsule. More quantitatively, representative temporal evolutions of cyst radius are shown in Fig. 3B (central panel) and Fig. S2.
Complementary experiments were performed to measure the characteristic time for hole closing, τhole. We were able to capture deflation events by chance (Movie 5). In parallel, we also carried out punching experiments with a micro-manipulator glass needles of typical diameter ∼10 μm (Movie 6). In both cases, deflation dynamics (Fig. S2) show that τhole is ∼1-2 min. As hypothesized in the rest of the manuscript, τgrowth≫τhole. All together, we see that whereas the free cyst oscillates in size with increasing average radius, after confluence the cyst is confined by the capsule and both of them oscillate jointly with a period longer than that observed during the free stage.
A qualitative test of our theory requires perturbation experiments to modulate the dynamics of cyst oscillations. This can be achieved either by molecular control of the permeation dynamics or by varying the external osmolarity. The former is not likely to shed any light on the general mechanisms as it would target specific membrane channels and cannot rule out the role of other compensatory mechanisms. Therefore, we performed the qualitative experiment of increasing the environmental osmolarity, and see that the elimination of an osmotic pressure difference completely inhibits cyst oscillations, consistent with our simple theory.
Adapting the model to experiments
with R1 being the maximum radius and ε1 the maximum strain before the first deflation and Δε=(σ2−σy)(1/H−1/E).
 htot=hc+ha. Because both layers are in contact, they undergo the same displacement. Assuming small variations in the thickness, and further that the thickness is much smaller than the radius, this implies that dRc/dt=dRa/dt. Using these approximations, we obtain a variant of the system of differential equations (Eqns 6-8) to describe the experimental system:
htot=hc+ha. Because both layers are in contact, they undergo the same displacement. Assuming small variations in the thickness, and further that the thickness is much smaller than the radius, this implies that dRc/dt=dRa/dt. Using these approximations, we obtain a variant of the system of differential equations (Eqns 6-8) to describe the experimental system:  , we obtained trajectories that fit the experimental results (Fig. 3B). This agreement shows that a simple but natural extension of our general model to account for plasticity of the tissue, and the elastic confinement by an alginate shell suffices to explain our experimental observations.
, we obtained trajectories that fit the experimental results (Fig. 3B). This agreement shows that a simple but natural extension of our general model to account for plasticity of the tissue, and the elastic confinement by an alginate shell suffices to explain our experimental observations.DISCUSSION
Size control requires the use of dynamic measurements to measure and control shape. As examples at the molecular scale, we point to microtubule length oscillations in asters, and at the cellular scale, we point to the ruffling oscillations in cells that are used to measure confluence. Here, we have presented a simple but general framework for tissue size control, inspired by the relatively common example of fluid-driven growth and hydraulically gated oscillations seen in diverse multicellular hollow tissue vesicles such as organoids, blastocysts, zebrafish inner ear and even body regeneration in H. vulgaris.
A crucial fact that underlies our study is that there is a large separation of time scales associated with the relatively fast rupture and leakage of luminal fluid when the tissue stress reached a critical value, and the slow growth of the lumen via permeation. This allows for robust regulation of cyst size via hydraulically gated oscillations. We present an analytical theory for the case of small strains in an elastic shell that yields simple expressions for the average size of the vesicle, and the frequency and amplitude of size oscillations, and complements a more general framework that accounts explicitly for complex mechanical properties and different functional forms for transport and growth. We also performed experiments in a synthetic set-up that showed the predicted oscillatory behavior, but to explain the gradual increase in the radius and the period of oscillation, we generalized our theory to include an elastic-plastic response for the tissue to describe the large strain behavior observed in our experiments.
The abrupt increase of the permeability of the cyst in our simple setting was associated with the formation of a simple hole. However, the pressure relief mechanism can take a variety of forms: localized channels, homogenous pores throughout the tissue or valves. Our coarse-grained model does not distinguish between these different mechanisms as long as the dynamics of opening and closure are faster than the cyst expansion and cell division rates, allowing us to model the outflow by an effective fast flux without focusing on the specifics. Natural extensions of this model include considerations of inhomogeneous spatial mechanical properties, active control of pressure relief via stretch-dependent valves, channels etc. and would allow us to understand how vesicular organs of a given size might be shaped by fluid pressure.
MATERIALS AND METHODS
Cell culture
We used wild-type MCF10DCIS.com cells (Asterand) and MCF10DCIS.com cells stably transfected with LifeAct-mCherry. Cells were maintained in DMEM-F12 (50:50) supplemented with 5% horse serum, 2 mM L-glutamine, and penicillin/streptomycin in a humidified atmosphere containing 5% CO2 at 37°C, with medium changed every 2 days. Culture media were purchased from Invitrogen and antibiotics from Gibco BRL.
Cell encapsulation
We used the Cellular Capsules Technology described by Alessandri et al. (2013). This method is based on a microfluidic co-extrusion device (Fig. 3A). The outer sheath is made of a sodium alginate solution and the inner core is composed of the cell suspension obtained after trypsinization of DCIS cells cultured in a Petri dish. Liquid extrusion is performed in the air with flow rates in the range of 50-100 ml/h, which leads to the formation of a jet that fragments into droplets (due to Plateau-Rayleigh instability). Because alginate undergoes gelation in the presence of divalent ions, composite droplets readily crosslink as shells encapsulating cells upon contact with a calcium bath. The intermediate capillary is filled with a calcium-free solution (e.g. sorbitol) that serves as a barrier to diffusion of calcium released from intracellular stores, and thus avoids blockage of the chip. Once cellular capsules were formed, they were transferred within 2 min into culture medium and placed inside an incubator (37°C, 5% CO2, ∼100% relative humidity). In each encapsulation run, several tens of capsules were selected for monitoring cyst morphology and growth using high-resolution imaging. A key property of the alginate hydrogel is its permeability (pore size of 10-15 nm), which allows free flow of oxygen and nutrients into the capsule and permits cell proliferation. In this jetting regime, the radius of the capsules is determined by the size of the injector nozzle, and the aspect ratio h/R (shell thickness/shell radius) is set by the ratio between outer and inner flow rates. In most experiments performed and analyzed in the present work, capsule radii were ∼100 µm and shell thicknesses were ∼20 µm. These morphological parameters were measured precisely by phase contrast microscopy for each individual capsule that was monitored for this work. As reported by Alessandri et al. (2013), the Young's modulus of alginate gels preformed in a 100 mM calcium bath and kept in culture medium for several days is E∼70 kPa.
Immunofluorescence, live imaging and image analysis
To characterize the structure of the growing cellular aggregates, the encapsulated cell cultures were incubated with 0.5 µg/ml fluorescent phalloidin (Molecular Probes) in PBS with 1% vol/vol Triton X-100 (Sigma) at 4°C from 2 h to overnight. Actin staining was complemented with labeling of apoptosis using fluorescent antibodies against Caspase 3 (Merck, AB3623) at 1 µg/ml. By confocal microscopy (LSM710; Carl Zeiss), we checked that the growing multicellular aggregates were hollow spheroids, i.e. cysts (Fig. S1). To monitor the growth dynamics of cysts, we mostly used phase contrast microscopy. Time-lapse sequences over extended periods of times (∼ 15 d) were acquired using an inverted microscope (Nikon Eclipse Ti, 10×/0.3 N.A. dry objective; Nikon Instruments) equipped with a motorized stage (Märzhäuser) and climate control system (The Brick; Life Imaging Systems). The microscope and camera (CoolSNAP HQ2; Photometrics) were driven by Metamorph software (Molecular Devices). Cyst radius measurements were obtained using ImageJ (National Institutes of Health). Live confocal imaging over shorter periods of time was also performed using an inverted (LSM710; Carl Zeiss) microscope. In this case, cysts were prepared with the MCF10DCIS.com LifeAct-mCherry stable line. Fluorescence was acquired using a 561-nm (15-mW) diode-pumped solid-state laser and a 25×/0.80 N.A. oil immersion objective.
Acknowledgements
We thank Philippe Chavrier and Catalina Lodillinsky for providing MCFDCIS cells, and Albrecht Ott for the images that constitute Fig. 1B.
Footnotes
Author contributions
Conceptualization: L.M., P.N.; Methodology: L.M., T.R.-H., P.N.; Software: T.R.-H.; Validation: L.M., T.R.-H., P.N.; Formal analysis: L.M., T.R.-H.; Investigation: L.M., T.R.-H., B.V.G., K.A., P.N.; Resources: P.N.; Data curation: B.V.G., K.A.; Writing - original draft: L.M., T.R.-H.; Writing - review & editing: L.M., T.R.-H., P.N.; Visualization: T.R.-H., B.V.G., K.A.; Supervision: L.M.; Project administration: L.M.; Funding acquisition: P.N.
Funding
This work was partially supported by the Agence Nationale de la Recherche (ANR) Invaders Project, and the Institut National de la Santé et de la Recherche Médicale Programme Physicancer Inserm 2011. T.R.-H. was supported by the Fundación Ramón Areces and the Simons Foundation.
References
Competing interests
The authors declare no competing or financial interests.